Functional Geometry of the Brain

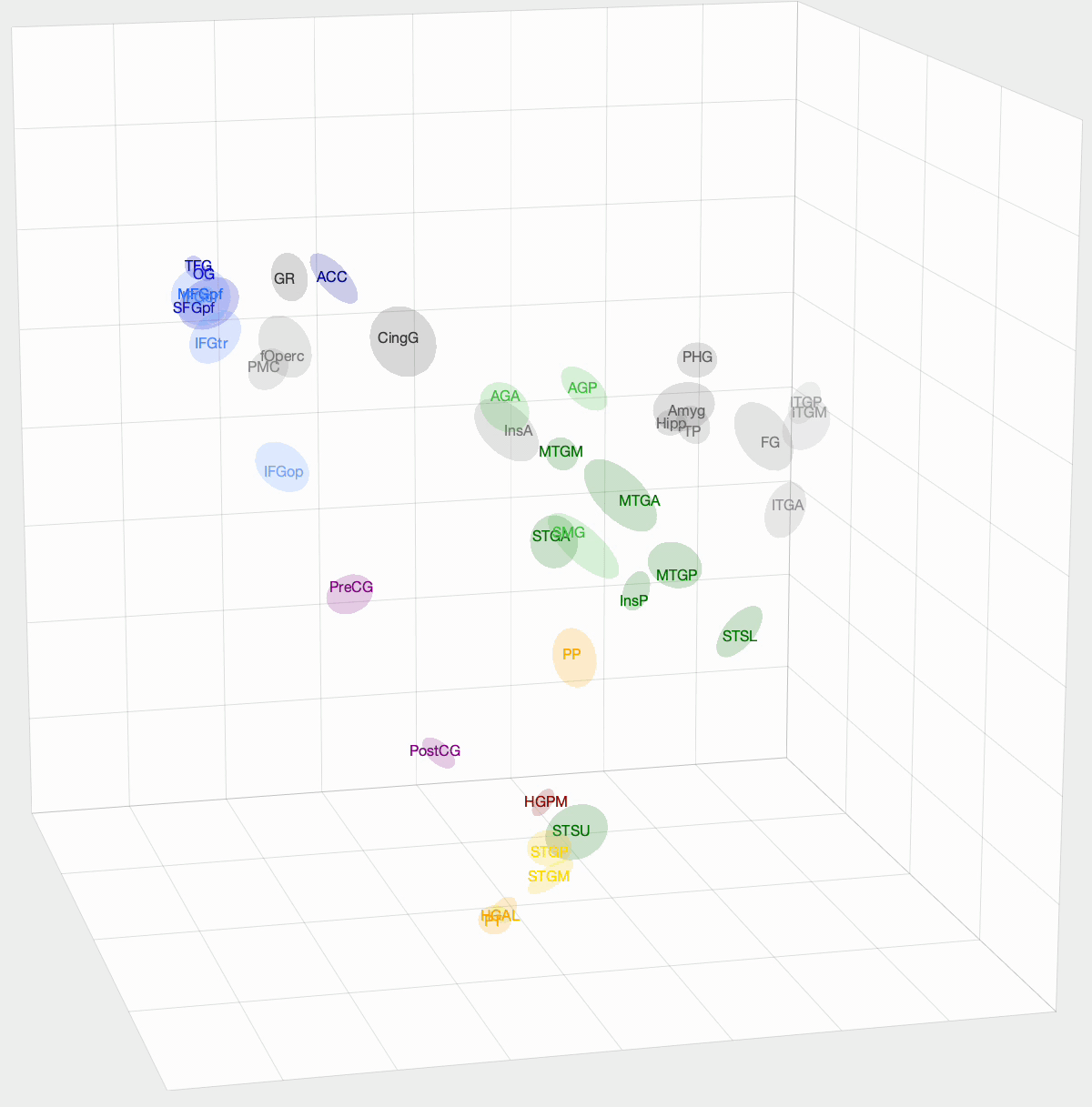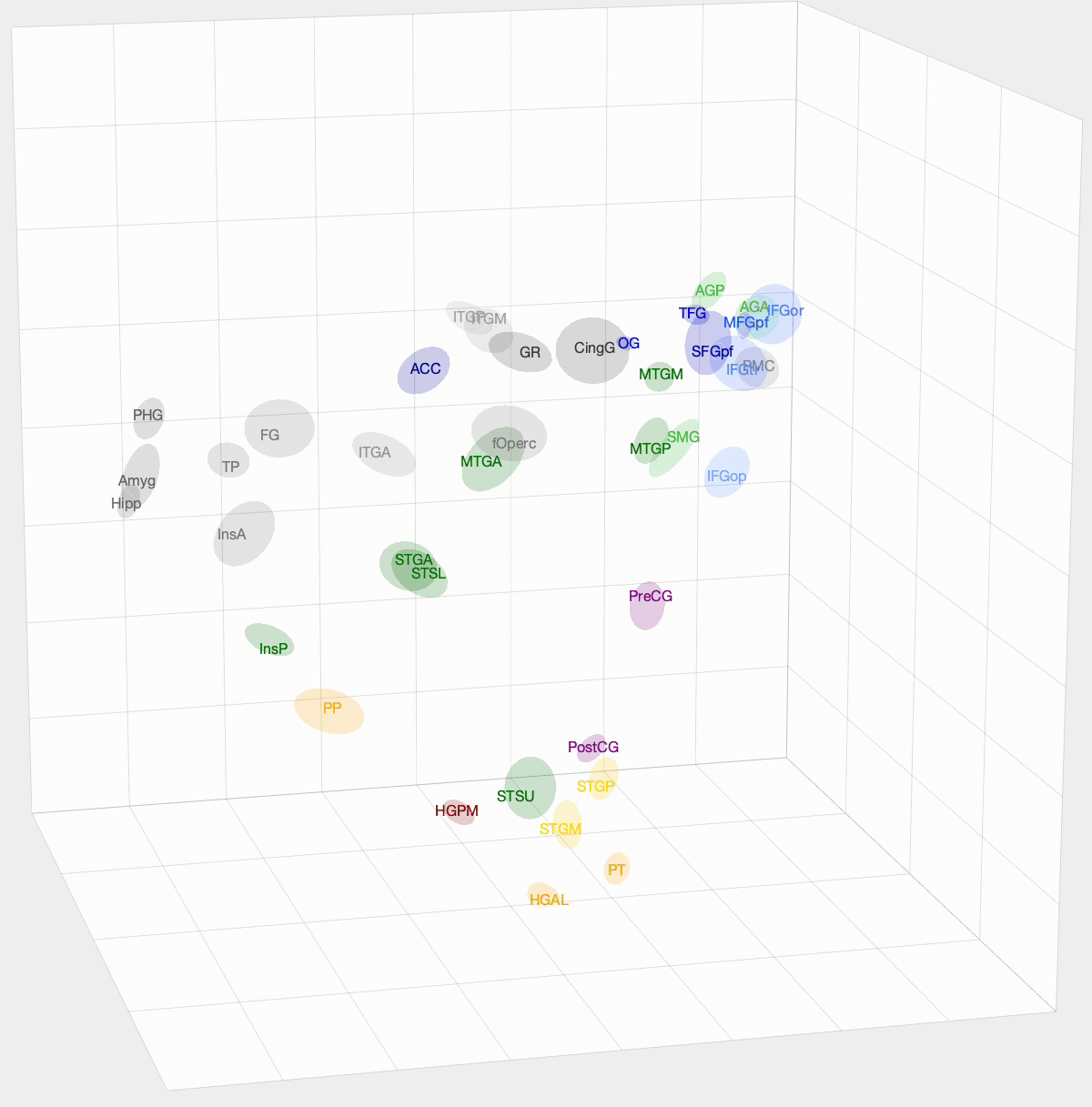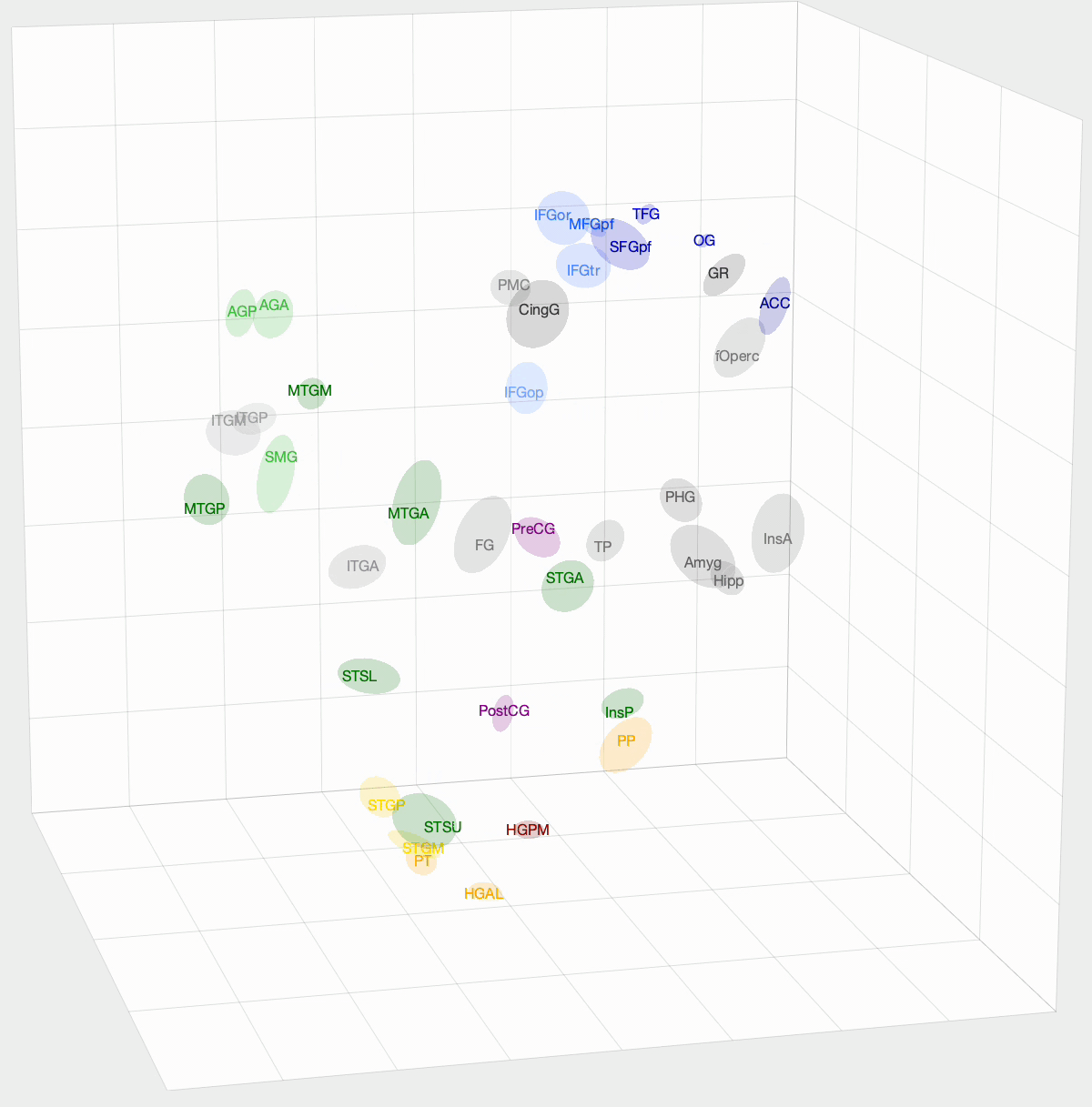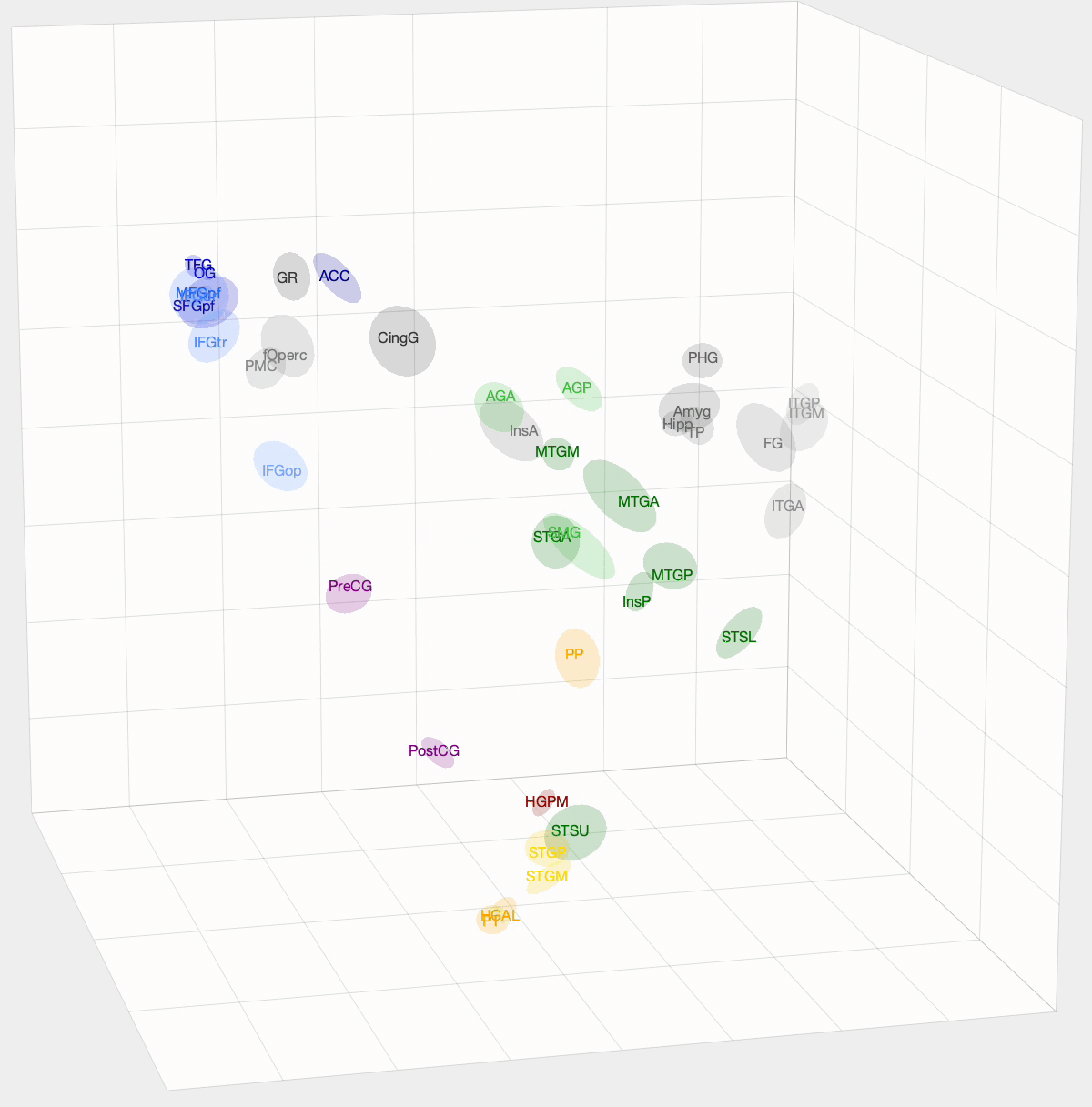
After InfoMap, the project I spent most of my time working on at Banks Lab involved using Diffusion Map Embedding to understand the underlying functional geometry of the brain. Inspired by high-dimensional data analysis, Diffusion Map Embedding assumes that your data lies on a low-dimensional structure or manifold. This method aims to map your data into a low-dimensional space, which uncovers its underlying geometry. There is some amazing math, mostly linear algebra, that goes into this method. If you want to know more about the math, check out these papers: Diffusion maps and Diffusion Maps for changing data.

We want to determine how functionally similar different regions of interest (ROIs) within the brain are. First, we create a Markov model of a given set of ROIs that we want to compare. We take the pairwise correlation between ROIs, then, after some preprocessing and normalization, we have a Markov model where an ROI pair’s transition probability is high if there is a correlation between their activation times. With Diffusion Map Embedding, we can map our Markov Model into ‘Diffusion Space,’ where Euclidean distance now equates to functional similarity in our Markov model. The closer two ROIs are, the more similar they are. This new space is N-dimensional, where N is the number of ROIs we are comparing. Each dimension doesn’t hold the same weight, though. For each dimension, there is a spectral value, where higher values mean that the dimension explains more variance in our data. From these values, we can determine how many dimensions we think explain the majority of variance in our data.

I used this method on functional magnetic resonance imaging (fMRI) and intracranial electrophysiological (iEEG) data to answer two questions: How similar are fMRI and iEEG data, and how does non-random sampling affect iEEG’s description of the brain? fMRI and iEEG both measure brain activity but in entirely different ways—one with magnetism and the other with voltage—so the question arises whether they capture the same information. I was able to show that there is some correlation, with an ~0.35 r-value. This value was skewed towards 0 due to outliers. For the second question, the problem with iEEG data is that you can never record from every ROI within a subject, and even within the ROI, you can’t cover the entire area. How does this sparse sampling affect the geometry that we are obtaining? I found that there is almost no information lost when using a subset of ROIs. However, sparse sampling of a given ROI does result in a worse description of that ROI, affecting the geometry of our embedding. The GIF above shows the averaged embedding across all iEEG patients, if you were wondering.